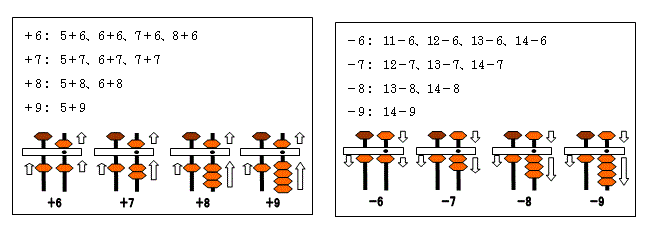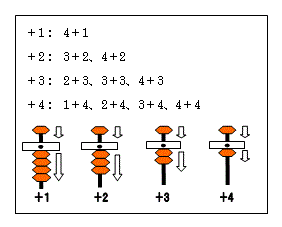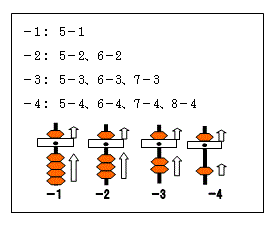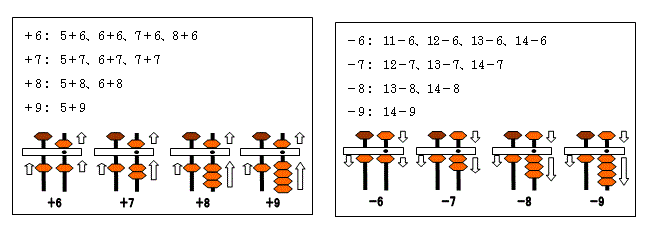Addition and Subtraction

Now you are all set to learn how to do basic calculations using soroban i.e. adding, subtracting etc in the following sections. Addition and subtraction of one digit numbers

First step of adding and subtracting 1～4

Basically, addition is performed by moving beads towards the crossbar by using thumb and subtraction is performed by moving a bead away from the crossbar as shown in the Figure. For example, addition and subtraction of 1, 2, 3 and 4 is done by moving up or down the 1, 2, 3, and 4 one-beads respectively.

First step of adding and subtracting 5～9

We learned above that the adding and subtracting numbers up to 4 can be done by using the one-beads. However, for adding numbers above 4, we need to use the five-beads.
Five-beads can be used by shifting them down to the cross bar. Moving it towards the cross bar means adding five and moving it away from the cross bar means subtracting five. You can use your forefinger for performing this task. Similarly, for adding 6 you need to move a five-bead and an one-bead towards the crossbar. Subtraction of 6 is done by moving the five-bead and a one-bead away from the crossbar.
Adding and subtracting numbers up to 9 can be done in the similar way. It would be easy to perform the calculation if you think that 7 is sum of 5 and 2, 8 is sum of 5 and 3 and 9 is sum of 5 and 4.

Second step of adding and subtracting 1～4

Having learnt the basic additions and subtractions, let us advance to little more advanced problems in this section. In this section, we will be performing operations indicated below.

4+1
3+2	4+2
2+3	3+3	4+3
1+4	2+4	3+4	4+4

Let us take the example of 4＋1. In order to perform this calculation, first you need to set 4 on your soroban. We need one more one-bead in order to add 1 to this value. However, we can see that the lower part of the column has no more one-beads left to be used.
All other problems are similar as there are no more beads left to perform this operation.

In order to overcome this problem, we need to use five-bead to perform the calculation.
Let us see how it can be done.
Let us think about the 4+1 problem once again. In this case, first we will set 4 on it by moving four one-beads towards the crossbar. Next, we take the help of five-bead just above in the same column by sliding it towards the crossbar. Now, on this column you will find one five-bead and four one-beads summing to 9 which is well above the addition we wanted to perform. Hence, now, we remove four by moving four one-beads away from the crossbar.

To begin with, this may look tricky and roundabout. However, there is a way to simplify this operation. That is by thinking that adding 1 is “adding 5 and removing 4” (1 = +5-4).

Similar is the case with the next example of 3+2. For this example, first we add three one-beads, then one five-bead, and then remove 3 one-beads. Adding 2, 3 and 4 can be solved in the similar way. Remember that adding 2 is “add 5, deduct 3”, adding 3 is “add 5, deduct 2” and adding 4 is “add 5, deduct 1”.

Here, it is important to observe the number of beads subtracted after adding 5. These numbers are called “complementary number to 5”.

1’s complementary number to 5 is 4
2’s complementary number to 5 is 3
3’s complementary number to 5 is 2
4’s complementary number to 5 is 1

Subtraction is completely opposite to that of addition. In addition we added 5 and removed the complementary number and in subtraction we add the complementary number and remove 5!

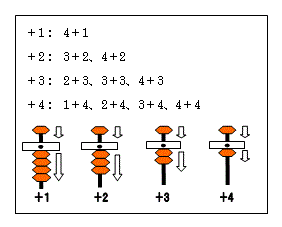
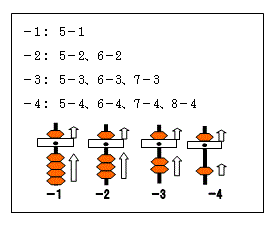
＜more further＞

Second step of adding and subtracting 6～9

Addition

In this section, let us calculate the problems listed below.

4＋6
4＋7	3＋7
4＋8	3＋8	2＋8
4＋9	3＋9	2＋9	1＋9

In these examples, we face a problem similar to that we learned to solve in the previous section. If you observe the examples above, you will easily find that there will not be enough beads to solve them using a single column. This necessitates us to use another column to solve the problem.

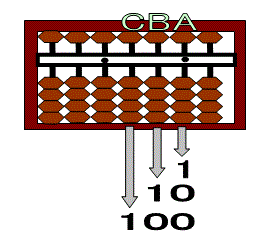
Let us recall some basics we learned on setting double digit numbers on the soroban. You know that the value of the digit increases as we move away on the left side of the ones column (Column A). This means that the Column B represents tens and the Column C represents hundreds and so on. Hence, adding one one-bead on the tens column (Column B) indicates 10 and two one-beads 20. Similarly, adding one one-bead on hundreds column (Column C) indicates 100 and four one-beads 400.

In order to solve the problems listed above, we need to obtain the complementary numbers to 10. The a's complementary number to 10 means the number lacks to make 10.In other word it's the difference between a and 10.
For example, 9 is 1 less than 10,it indicates that 9's complementary number to10 is 1. Similarly, you can also obtain the 8’s complementary number’s to10 as 2, 7’s complementary number’s to10 as 3 and 6’s complementary number to 10 as 4.

9’s complementary number to 10 is 1
8’s complementary number to 10 is 2
7’s complementary number to 10 is 3
6’s complementary number to 10 is 4

Let us take the example of 4＋9. For solving this problem, first, we set 4 on the ones column(Column A). We can see that this column does not have sufficient beads to add 9 to 4. This makes us to use tens column (Column B) by shifting up one one-bead on it. Now we can see that Soroban shows 14 on it which is higher than we expected. We need to remove some beads exceeded on the ones column. We were trying to add 9, but add 10. It means we did add 1 more than we expected, as a result we need to remove a bead on the ones column. you can see that the Soroban shows 13 as an output. The number deducted on the ones column is that the complementary number to 10. In this case 1, the number we deducted on the ones column, is the complementary number of 9 we wanted to add.

In this example we explained 4＋9 as "add 10 and subtract 1", but it is NOT a normal way to solved it. We have a common rule that is “deduct the complementary number on ones column and add one on tens column”. Following this rule, first we shoul deduct 1(this is a complementary number of 9) and move one bead up on the ten's column, and then we can obtain the correct answer of 4+9 as 13.

Let us consider another example of 4+6. For solving this problem, first add four on ones column. Now we can see that the ones column doesn’t have sufficient beads to add 6. Following the rule “deduct 4 ones column and add one on tens column”, you can see that the Soroban shows 10 as result.

Please remember that the order of performing calculation on Soroban is very important as subtracting a complementary number is to be done first and then addition of 10 on tens column.

Subtraction

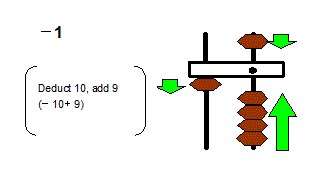
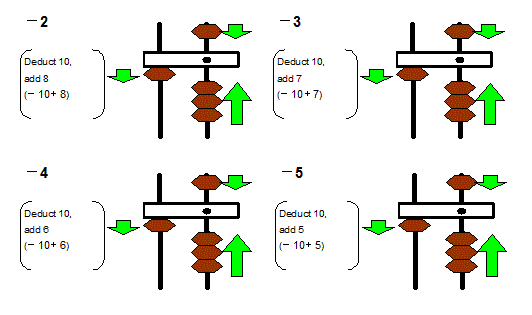
As we learned earlier, subtraction is completely opposite to the addition. Addition is subtracting complementary number and adding 10 while subtraction involves subtracting 10 and adding the complementary number. Here are some pictures showing subtraction operation involving numbers -9 to -6.

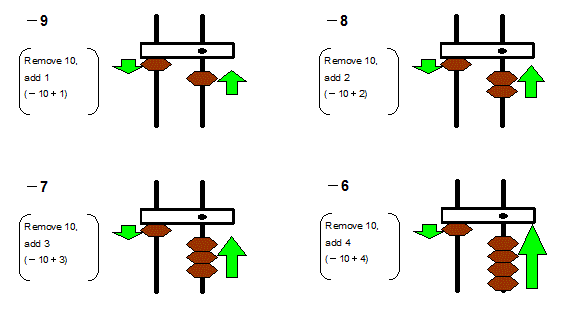
Third step of adding and subtracting 1～5

Addition

This is the third step to solve the problems listed below. These all involve using two digit numbers and procedure is same as we learned in the previous section i.e. “subtract a complementary number and add 10” In this section, let us learn to solve some of the following problems:

9＋1
9＋2	8＋2
9＋3	8＋3	7＋3
9＋4	8＋4	7＋4	6＋4
9＋5	8＋5	7＋5	6＋5	5＋5

Let us revise the complementary numbers of 1～5 to ten.

1’s complementary number to10 is 9.
2’s complementary number to10 is 8.
3’s complementary number to10 is 7.
4’s complementary number to10 is 6.
5’s complementary number to10 is 5.

Now, let’s take an example of 9＋1. Now, set your ones column to nine. You can see that there are no enough beads to add one. Hence, subtract the complementary number of 1 i.e. 9 and add 10 by adding one on tens column.

Likewise, you can add 2, 3, 4, and 5 to 9 now. Adding 2 is “deduct 8 and add 10”, adding 3 is “deduct 7 and add 10”, adding 4 is “deduct 6 and add 10”, and adding 5 is “deduct 5 and add 10.” These calculations are depicted in the following pictures.

Subtraction

In this case also, subtraction is quite apposite to the addition. Subtract 1 is “deduct 10, add 9”, subtract 2 is “deduct 10, add 8”, subtract 3 is “deduct 10, add 7” subtract 4 is “deduct 10, add 9” subtract 5 is “deduct 10, add 5”.

Third step of adding and subtracting 6～9

Addition

Third step of adding and subtracting 6～9 Addition: This is the last section of addition and subtraction. In this section, we will learn to solve the following problems:

5＋6	6＋6	7＋6	8＋6
5＋7	6＋7	7＋7
5＋8	6＋8
5＋9

Now let’s solve 5＋6. After setting 5 on ones column we will add six to it but recognize that there are no enough beads to add 6. We know that 6 is 5+1. Hence, we add 1 and apply the thumb rule “adding 5 is subtracting 5 and adding ten.” Following this rule you can see that the answer is 11!

This problem can be solved from a different angle by considering that adding 6 is subtracting 4 and adding 10. To solve this way, you need to set 5 on ones column, subtract 4, and add ten by adding one on tens column. Looking at these two ways, you recognize that the answers are completely same. The following pictures show the third step of adding 5 to 9.

Subtraction

Here also the subtraction is opposite to that of addition. Let us quickly look at the thumb rules for subtraction. Subtracting 6 is “deduct 10, add 5 and deduct 1”, subtracting 7 is “deduct 10, add 5 and deduct 2”, subtracting 8 is “deduct 10, add 5 and deduct 3”, and subtracting 9 is “deduct 10, add 5 and deduct 4.”

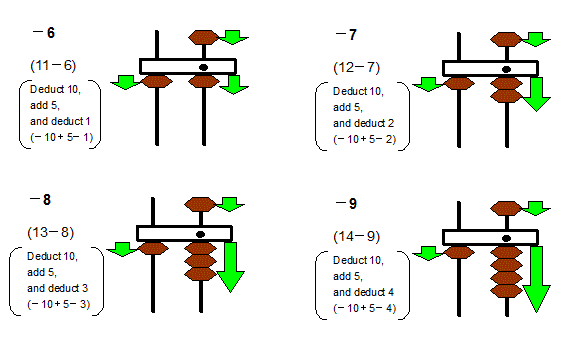
The following pictures show the third step of subtraction from 5 to 9.

11－6	12－6	13－6	14－6
12－7	13－7	14－7
13－8	14－8
14－9

Those are last10 problems. Now you can calculate all addition and subtraction one digit numbers.